آمار توصیفی چیست؟
در هر پژوهش و تحقیقی بعد از جمع آوری داده ها، نیاز است داده های جمع آوری شده، مورد بررسی قرار گیرد. اولین گام در بررسی داده ها ، ساده سازی داده های نمونه است. این ساده سازی باید به گونه ای باشد که تصویری کلی از مجموعه داده ها در اختیار محقق قرار دهد.
آمار توصیفی بخشی از علم آمار است که روش های خلاصه کردن و توصیف الگوی کلی داده ها را بیان می کند. آمار توصیفی به ما کمک می کند تا حجم زیادی از داده ها را به روشی معقول ساده کنیم. با استفاده از آمار توصیفی امکان تفسیر ساده تر داده ها فراهم می شود و به راحتی پی می بریم که در داده هایمان چه می گذرد.
آمار توصیفی با ارائه جداول و نمودارها، بیان ویژگی های مهم داده ها از جمله تقارن یا انحراف از تقارن، مشخص کردن داده های پرت و دور از انتظار، محاسبه معیارهای عددی مثل شاخص های مرکزی و شاخص های پراکندگی، نمای کلی از داده های در دست بررسی را ترسیم می کند.
جداول و نمودارها در آمار توصیفی
با استفاده از تجزیه و تحلیل های گرافیکی ساده می توان تصویری کلی از داده ها را به دست آورد. آمار توصیفی با استفاده از جداول توزیع فراوانی و توصیف های گرافیکی با استفاده ار رسم نمودار و چارت ها شکل توزیع و پراکندگی داده ها را نمایش می دهد. این نمودارها شامل نمودار نقطه ای(point chart)، نمودار پراکندگی(scatter plot)، نمودار میله ای(bar chart)، هیستوگرام یا بافت نگار(histogram) و … است.
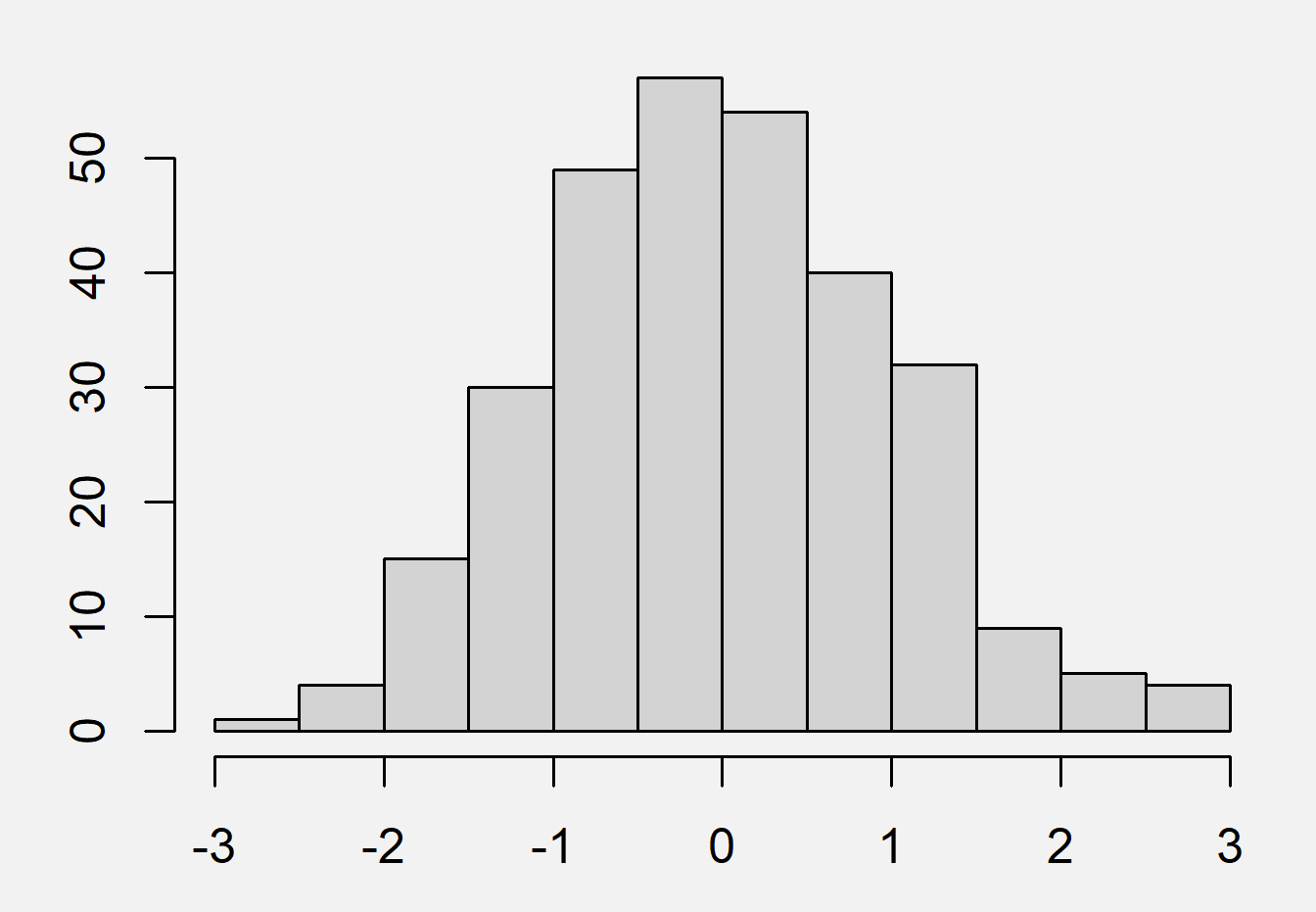
بافت نگار
معیارهای گرایش مرکزی
معیارهای گرایش مرکزی موقعیت مرکزی داده ها را مشخص می کنند. میانگین(mean)، میانه(median)، چارک ها(quartile)، صدک ها(percentile) و نما یا مد (mode) معیارهای گرایش مرکزی هستند. در شرایط مختلف، برخی از معیارهای گرایش مرکزی مناسب تر از بقیه هستند.
میانگین معروفترین و مهمترین معیار گرایش مرکزی است. می توان آن را هم با داده های گسسته و هم با داده های پیوسته استفاده کرد، اگرچه استفاده از آن اغلب با داده های پیوسته است (راهنمای انواع متغیر ها برای انواع داده ها را ببینید). میانگین برابر است با مجموع همه مقادیر موجود در مجموعه داده ، تقسیم بر تعداد مقادیر موجود در مجموعه داده.
علیرغم اینکه میانگین رایج ترین معیار مرکزی است و خطا را در پیش بینی ها به حداقل می رساند اما گاهی استفاده از آن مناسب نیست. نقطه ضعف میانگین این است که در معرض داده های پرت قرار دارد. داده های پرت مقادیری هستند که در مقایسه با بقیه مجموعه داده ها به دلیل کوچک یا بزرگ بودن مقادیرعددی، غیرعادی هستند. در این شرایط میانه می تواند معیار بهتری برای اندازه گیری مرکز داده ها باشد.
میانه رقمی است که در وسط مجموعه داده قرار دارد. میانه اندازه وسط مجموعه ای از داده ها است که به ترتیب بزرگی مرتب شده اند. در واقع میانه داده ای است که پنجاه درصد مشاهدات از آن کوچکتر و پنجاه درصد از آن بزرگتر هستند.
زمانی که دادههای ما دارای انحراف هستند معمولاً میانه را بر میانگین ترجیح میدهیم (یعنی توزیع فراوانی برای دادههای ما منحرف است). وقتی که داده ها کاملا نرمال هستند، میانگین، میانه و نما یکسان هستند. علاوه بر این، همه آنها معمولی ترین مقدار را در مجموعه داده ها نشان می دهند. اما، وقتی توزیع دادهها کج باشد، میانگین دیگر بهترین مکان مرکزی دادهها را ارائه نمی کند، در حالی که، میانه به بهترین وجه این موقعیت را حفظ می کند و خیلی تحت تأثیر مقادیر منحرف نیست.
می توان داده ها را به ترتیب بزرگی مرتب کرده و به چهار قسمت تقسیم کرد، نقاط تقسیم داده ها به چهار قسمت را چارک می نامند. البته بر همین اساس می توان دهک ها و صدک ها را نیز محاسبه کرد.
نما داده ای است که بیشترین تکرار را دارد.
روش محاسبه شاخص های مرکزی با مثال را اینجا مطالعه کنید.
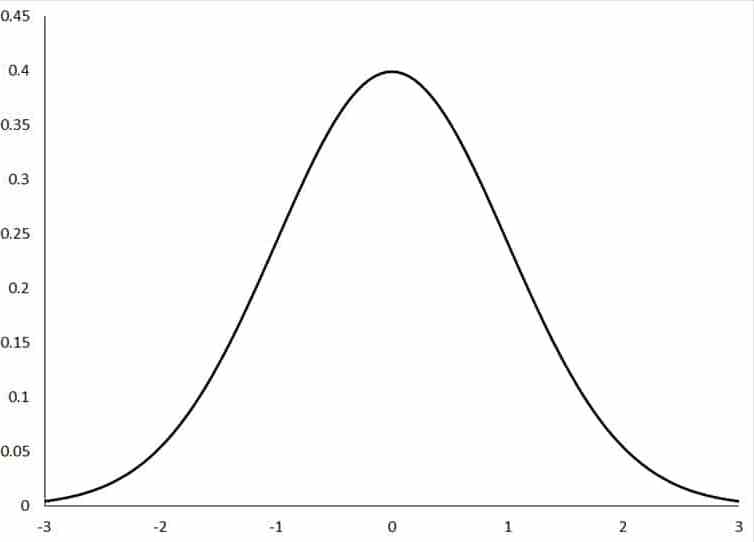
توزیع نرمال
شاخص های پراکندگی
شاخص های پراکندگی شامل دامنه(range)، واریانس(variance) و انحراف معیار(standard deviation) است. این شاخص ها تصویری عددی از میزان پراکندگی ها نشان می دهند. فرض کنید میانگین نمرات 100 دانشجو، نمره 17 باشد. مسلم است که همه دانشجوها نمره 17 کسب نکرده اند بلکه نمرات حول این مقدار میانگین پراکنده اند. معیارهای پراکندگی کمک می کنند میزان این پراکندگی را خلاصه کنیم. دو مجموعه داده ممکن است میانگین های یکسانی داشته، اما از نظر پراکندگی متفاوت باشند.
در کنار این شاخص ها دو معیار چولگی(Skewness) و کشیدگی (kurtosis) شکل توزیع داده ها را با استفاده از اعداد نشان می دهند.
اگر مجموع مربعات اختلاف هر داده ها از میانگین، را بر تعداد داده ها منهای یک، تقسیم کنیم واریانس به دست می آید. به زبان ساده تر برای محاسبه واریانس ابتدا اختلاف هر داده را از میانگین محاسبه کرده سپس به توان دو رسانده و با هم جمع می کنیم. در نهایت حاصل را بر تعداد داده ها منهای یک تقسیم می کنیم. با توجه به اینکه در محاسبه واریانس از توان های دوم استفاده می شود واحد اندازه گیری آن، توان دوم واحدی است که داده های اولیه دارند. مثلاً اگر داده بر حسب متر باشند واریانس بر حسب 2(متر) خواهد بود. بنابراین برای اینکه واحد اندازه گیری معیار پراکندگی با واحد اندازه گیری داده ها یکسان باشد از واریانس جذر مثبت گرفته می شود. این شاخص اندازه گیری انحراف معیار نامیده می شود.
دامنه نمونه نیز یکی دیگر از معیارهای پراکندگی است و فاصله ای که مشاهدات در آن پراکنده شده اند را نشام می دهد. این شاخص از اختلاف بزرگترین و کوچکترین مشاهده به دست می آید. محاسبه این شاخص بسیار ساده است و اغلب زمانی به کار می رود که حجم نمونه خیلی کوچک باشد. این شاخص بسیار تحت تاثیر مقادیر خیلی کوچک و خیلی بزرگ یا داده های پرت قرار دارد و در تمام حالات نقاط میانی داده ها را نادیده می گیرد.
برای حذف اثر داده های دور افتاده و پرت از شاخص دیگری به نام دامنه میان چارکی استفاده می شود. دامنه میان چارکی از اختلاف چارک سوم و چارک اول به دست می آید. وجود داده های خیلی بزرگ و خیلی کوچک تاثیری بر این شاخص ندارد. در مجموعه داده هایی که توزیع های کشیده دارند دامنه میان چارکی معیار بهتری برای سنجش پراکندگی داده های نمونه خواهد بود.
برای یادگیری محاسبه شاخص های پراکندگی با استفاده از مثال اینجا را مطالعه کنید.
چولگی(Skewness)
چولگی شاخصی است که تقارن یا عدم تقارن تابع توزیع یک متغیر را نشان می دهد. در صورتی که توزیع یک متغیر نسبت به میانگین آن کاملا متقارن باشد چولگی صفر خواهد بود. در توزیع نامتقارن اگر حجم داده های بیشتری در سمت راست متمرکز شده باشند کشیدگی به سمت مقادیر کوچکتر بوده و چولگی منفی می شود(چوله به چپ) اما اگر حجم داده ها بیشتر در سمت چپ متمرکز شوند کشیدگی به سمت مقادیر بزرگتر خواهد بود و چولگی مثبت می شود(چوله به راست).
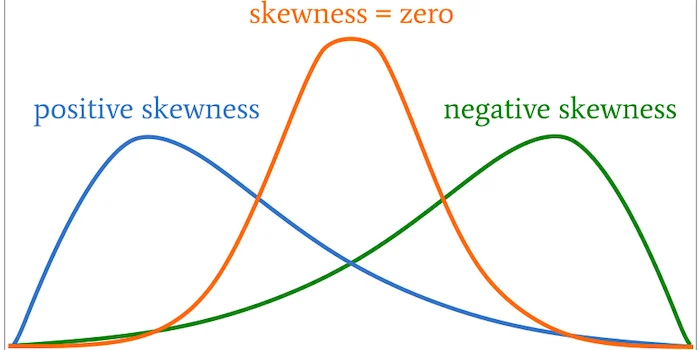
چولگی
کشیدگی (kurtosis)
کشیدگی شاخصی است که برای بررسی و مقایسه ارتفاع تابع توزیع متغیر مورد استفاده قرار می گیرد. این شاخص نشان دهنده میزان قله ای یا مسطح بودن یک توزیع است. هرچه شکل تابع توزیع قله ای تر باشد میزان کشیدگی آن بیشتر خواهد بود.
در توزیع نرمال کشیدگی برابر صفر است. در صورتی که تابع توزیع از توزیع نرمال برآمده تر باشد کشیدگی مثبت و اگر مسطح تر باشد کشیدگی منفی می شود.
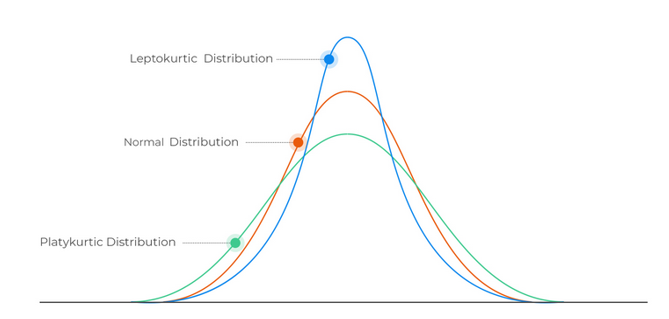
کشیدگی
با استفاده از این دو شاخص می توان توزیع یک متغیر را با توزیع نرمال مورد مقایسه قرار داد. در حالت کلی اگر چولگی و کشیدگی در بازه (2، 2-) قرار نگیرد نمی توان گفت توزیع آن نرمال است.
چگونه یک معیار عددی مناسب برای توصیف داده ها انتخاب کنیم؟
برای انتخاب معیار عددی مناسب که داده ها را به خوبی توصیف و خلاصه کند توجه به نکات زیر لازم است.
*توجه به هدفی که از توصیف و خلاصه سازی داده ها داریم.
*تحت تاثیر مشاهدات دور از انتظار قرار نگرفتن
*کاربرد شاخص در انجام استنباط های آماری
*نوع متغیر و داده مورد بررسی
*امکان تعبیر و تفسیر ساده
ابزار مناسب برای محاسبه شاخص های توصیفی
با افزایش حجم داده ها، انجام محاسبات دستی مشکل، زمانبر و با خطا همراه خواهد شد. با پیشرفت علم و تکنولوژی، نرم افزارهای کامپیوتری مختلفی به عنوان ابزاری برای تسهیل در انجام محاسبات ایجاد شده اند. یکی از بهترین این ابزارها که کار با آن بسیار آسان است، نرم افزار spss است.
با یادگیری این نرم افزار می توانید محاسبات آماری خود را با حداکثر دقت و سهولت انجام دهید.
