نرمالسازی دادهها (Min-Max و Z-Score) — کدام روش برای چه نوع دادهای مناسب است؟
در تحلیل داده و یادگیری ماشین، نرمالسازی دادهها یک مرحله اساسی برای بهبود عملکرد مدلهاست. دو روش پرکاربرد نرمالسازی، Min-Max و Z-Score هستند. اما کدام روش برای چه نوع دادهای مناسب است؟ در این مقاله، به تفاوت این دو روش، مزایا و معایب هرکدام و کاربردهایشان میپردازیم.
1. نرمالسازی چیست و چرا مهم است؟
نرمالسازی فرآیند تغییر مقیاس دادهها به یک محدوده استاندارد است تا:
- از تأثیر غیرمنصفانه ویژگیهای با مقیاس بزرگ جلوگیری کند.
- الگوریتمهای یادگیری ماشین را بهبود بخشد (مثل KNN، شبکههای عصبی).
- مقایسه بین متغیرها را آسانتر کند.
2. روش Min-Max (نرمالسازی مبتنی بر محدوده)
این روش دادهها را به بازه [۰, ۱] یا [a, b] منتقل میکند.
📌 فرمول:
 مزایای Min-Max:
مزایای Min-Max:
- ساده و قابل فهم است.
- برای دادههای با توزیع یکنواخت مناسب است.
- در الگوریتمهایی که به محدوده مشخصی نیاز دارند (مثل شبکههای عصبی) مفید است.
معایب Min-Max:
- به outliers (مقادیر پرت) حساس است.
- اگر دادهها گسترده باشند، ممکن است تفاوتهای کوچک از بین بروند.
چه زمانی از Min-Max استفاده کنیم؟
✅ دادههایی با توزیع یکنواخت و بدون outlier (مثل نمرات دانشجویان، درصدها).
✅ زمانی که نیاز داریم دادهها در یک بازه مشخص باشند (مثل تصاویر با پیکسلهای ۰ تا ۲۵۵).
مثال:
فرض کنید دادههای ما [۱۰, ۲۰, ۳۰, ۴۰] هستند.
Min(X) = ۱۰
Max(X) = ۴۰
نرمالسازی عدد ۲۰:
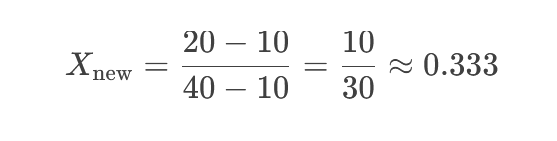 پس از نرمالسازی، دادهها به این صورت خواهند بود:
پس از نرمالسازی، دادهها به این صورت خواهند بود:
[۰, ۰.۳۳۳, ۰.۶۶۶, ۱]
✅ نتیجه: ۰.333 (در بازه [۰, ۱]).
مثال:
اگر بخواهیم داده [۲۰] را به بازه [۱۰, ۲۰] تبدیل کنیم: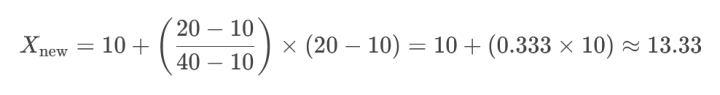
3. روش Z-Score (استانداردسازی)
روش Z-Score (یا استانداردسازی) دادهها را بر اساس میانگین (μ) و انحراف معیار (σ) تبدیل میکند. این روش، توزیع دادهها را به شکلی درمیآورد که میانگین آنها ۰ و انحراف معیارشان ۱ شود. این کار برای مقایسه دادههایی که واحدهای مختلفی دارند یا مقیاسشان متفاوت است، بسیار مفید است.
📌 فرمول:
X: مقدار اصلی داده
μ (میانگین): متوسط مقادیر دادهها
σ (انحراف معیار): میزان پراکندگی دادهها حول میانگین
X<sub>new</sub>: مقدار استانداردشده (Z-Score)
مزایای Z-Score:
- نسبت به outliers مقاومتر است.
- برای دادههای با توزیع نرمال یا نزدیک به نرمال مناسب است.
- در روشهای آماری مانند رگرسیون خطی بهتر عمل میکند.
معایب Z-Score:
- محدوده خروجی ثابتی ندارد (ممکن است اعداد خیلی بزرگ یا کوچک شوند).
- اگر دادهها بسیار پراکنده باشند، ممکن است همچنان مشکلساز شود.
چه زمانی از Z-Score استفاده کنیم؟
✅ دادههایی با توزیع نرمال یا نزدیک به نرمال (مثل قد افراد، IQ).
✅ زمانی که outlierها وجود دارند ولی نمیخواهیم حذفشان کنیم.
مثال:
Z-Score:
فرض کنید دادههای ما [۱۰, ۲۰, ۳۰, ۴۰] باشند.
۱. محاسبه میانگین (μ):
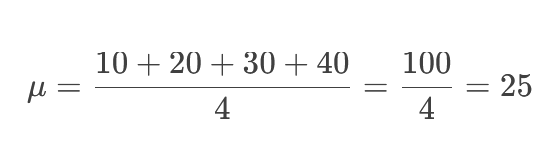 ۲. محاسبه انحراف معیار (σ):
۲. محاسبه انحراف معیار (σ):
واریانس (σ²): میانگین مربع اختلاف هر داده از میانگین

 انحراف معیار (σ): ریشه دوم واریانس
انحراف معیار (σ): ریشه دوم واریانس
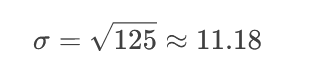 ۳. محاسبه Z-Score برای عدد ۲۰:
۳. محاسبه Z-Score برای عدد ۲۰:
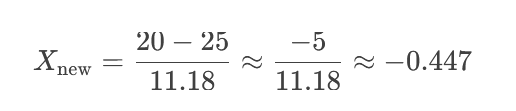 نتیجه نهایی (Z-Score همه دادهها):
نتیجه نهایی (Z-Score همه دادهها):

4. مقایسه Min-Max و Z-Score
| ویژگی | Min-Max | Z-Score |
|---|---|---|
| محدوده خروجی | [۰, ۱] یا [a, b] | محدوده ثابتی ندارد |
| حساسیت به outlierها | بالا | کم |
| توزیع مناسب | یکنواخت | نرمال |
| کاربردهای رایج | پردازش تصویر، شبکههای عصبی | رگرسیون، خوشهبندی |
5. کدام روش را انتخاب کنیم؟
🔹 از Min-Max استفاده کنید اگر:
- دادههای شما محدوده مشخصی دارند (مثل درصدها، رنگهای دیجیتال).
- میخواهید دادهها در یک مقیاس ثابت باشند.
- outlierها کم هستند یا حذف شدهاند.
🔹 از Z-Score استفاده کنید اگر:
- دادهها توزیع نرمال دارند یا نزدیک به نرمال هستند.
- داده های پرت وجود دارند و نمیخواهید حذفشان کنید.
- از روشهای آماری مانند PCA یا رگرسیون استفاده میکنید.
6. جمعبندی
- Min-Max برای دادههای محدود و یکنواخت مناسب است.
- Z-Score برای دادههای نرمالشده و مقاومت در برابر داده های پرت بهتر است.
- انتخاب روش به نوع داده و نیاز مدل بستگی دارد.
اگر نیاز به راهنمایی بیشتر دارید یا سوالی درباره نرمالسازی دارید، در بخش نظرات بپرسید! 😊

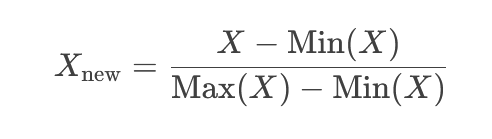 مزایای Min-Max:
مزایای Min-Max: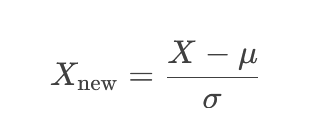
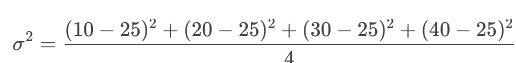
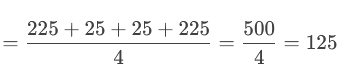 انحراف معیار (σ): ریشه دوم واریانس
انحراف معیار (σ): ریشه دوم واریانس