معیارهای پراکندگی در آمار: مفاهیم، فرمولها و کاربردها
مقدمه: چرا اندازهگیری پراکندگی دادهها مهم است؟
در تحلیل دادهها، تنها دانستن میانگین یا میانه کافی نیست. دو مجموعه داده با میانگین یکسان ممکن است رفتار کاملاً متفاوتی داشته باشند. معیارهای پراکندگی (Measures of Dispersion) ابزارهایی هستند که میزان گستردگی و تغییرپذیری دادهها حول مرکز توزیع (مانند میانگین) را کمّی میکنند. این معیارها در حوزههایی مانند اقتصاد، علوم اجتماعی، مهندسی کنترل کیفیت و یادگیری ماشین کاربرد حیاتی دارند.
در این مقاله جامع، به بررسی ۷ شاخص کلیدی پراکندگی میپردازیم:
۱. دامنه تغییرات (Range)
۲. واریانس (Variance)
۳. انحراف معیار (Standard Deviation)
۴. انحراف میانگین (Mean Absolute Deviation)
۵. ضریب تغییرات (Coefficient of Variation)
۶. محدوده بینچارکی (Interquartile Range)
۷. انحراف چارکی (Quartile Deviation)
۱. دامنه تغییرات (Range): سادهترین شاخص پراکندگی
تعریف و فرمول
دامنه تغییرات سادهترین شاخص پراکندگی است که اختلاف بین بزرگترین و کوچکترین مقدار در مجموعه دادهها را نشان میدهد:
 مثال کاربردی
مثال کاربردی
برای دادههای [۲, ۵, ۷, ۱۲, ۱۵]:
 مزایا و محدودیتها
مزایا و محدودیتها
✅ مزیت: محاسبه سریع و ساده
❌ محدودیت: به مقادیر پرت (Outliers) بسیار حساس است. اگر کوچکترین یا بزرگترین داده تغییر کند، دامنه به شدت تحت تأثیر قرار میگیرد.
۲. واریانس (Variance): معیار پراکندگی مبتنی بر مربع انحرافات
تعریف و فرمول
اگر اختلاف هر داده را از میانگین داده ها محاسبه و آنها را با هم جمع کنیم حاصل آن صفر خواهد شد. بنابراین برای اینکه بتوانیم پراکندگی داده ها حول میانگین را محاسبه کنیم اختلاف هر داده از میانگین را به توان دو می رسانیم و سپس مجموع را محاسبه می کنیم و سپس بر تعداد داده ها تقسیم می کنیم. به این شکل می توان شاخصی برای میزان پراکندگی داده ها حول میانگین به دست آورد.
واریانس میانگین مربع اختلاف هر داده از میانگین را محاسبه میکند. دو نوع واریانس داریم:
واریانس جامعه آماری:
 واریانس نمونه:
واریانس نمونه:
 مثال محاسبه
مثال محاسبه
برای دادههای [۳, ۷, ۷, ۱۹] (به عنوان جامعه):
میانگین
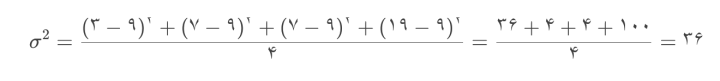
نکات کلیدی
🔹 واحد واریانس، مربع واحد داده اصلی است (مثلاً اگر داده بر حسب کیلوگرم باشد، واریانس بر حسب kg² خواهد بود).
🔹 هرچه واریانس بزرگتر باشد، پراکندگی دادهها بیشتر است.
۳. انحراف معیار (Standard Deviation): پرکاربردترین شاخص پراکندگی
یکی از مشکلات در نظر گرفتن واریانس به عنوان شاخص پراکندگی در توصیف داده ها این است که واحد واریانس، مربع واحد داده اصلی است، بنابراین برای رفع این موضوع و رسیدن به مقیاس درست اندازه گیزی از واریانس جذر (ریشه دوم) می گیریم. مثلاً اگر داده بر حسب متر باشد، واریانس بر حسب m² خواهد بود و با گرفتن ریشه دوم می توان پراکندگی را بر حسب متر بیان کرد.
تعریف و فرمول
انحراف معیار ریشه دوم واریانس است و واحد آن با داده اصلی یکسان است:
 مثال
مثال
برای دادههای بخش قبل:
 کاربردهای انحراف معیار
کاربردهای انحراف معیار
قاعده ۶۸-۹۵-۹۹.۷: در توزیع نرمال:
۶۸٪ دادهها در محدوده μ±σ
۹۵٪ در μ±۲σ
۹۹.۷٪ در μ±۳σ
مقایسه پراکندگی دو مجموعه داده با واحدهای مشابه
۴. انحراف میانگین (MAD): معیار مقاوم به پرت
تعریف و فرمول
میانگین قدر مطلق انحرافات از میانگین یا میانه:
 مثال
مثال
برای دادههای [۲, ۴, ۶, ۸, ۱۰]:
میانگین X
 مزیت کلیدی
مزیت کلیدی
🔹 نسبت به واریانس، حساسیت کمتری به مقادیر پرت دارد.
۵. ضریب تغییرات (CV): مقایسه پراکندگی در واحدهای مختلف
تعریف و فرمول
نسبت انحراف معیار به میانگین، بیانگر پراکندگی نسبی:
 مثال کاربردی
مثال کاربردی
مجموعه A: میانگین = ۵۰، انحراف معیار = ۵ →
مجموعه B: میانگین = ۲۰۰، انحراف معیار = ۲۰ →
با وجود تفاوت در مقیاس، پراکندگی نسبی یکسان است.
۶. محدوده بینچارکی (IQR): معیار پراکندگی برای دادههای نامتقارن
تعریف و فرمول
اختلاف بین چارک سوم (Q3) و چارک اول (Q1):
IQR=Q۳−Q
شناسایی دادههای پرت با IQR
دادههای خارج از محدوده زیر را میتوان پرت در نظر گرفت:
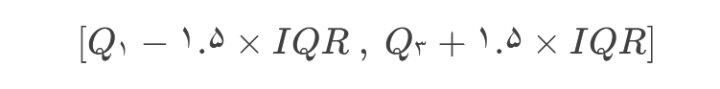
نتیجهگیری: چگونه معیار مناسب را انتخاب کنیم؟
| معیار پراکندگی | مناسب برای | مقاوم به پرت | واحد اندازهگیری |
|---|---|---|---|
| دامنه تغییرات | دادههای ساده | خیر | همانند داده اصلی |
| واریانس | محاسبات آماری | خیر | مربع واحد داده |
| انحراف معیار | توزیعهای نرمال | خیر | همانند داده اصلی |
| MAD | دادههای با پرت | بله | همانند داده اصلی |
| IQR | دادههای نامتقارن | بله | همانند داده اصلی |
برای یادگیری بیشتر مباحث آماری، مقالات آموزشی ما را درtarjomanamar.ir دنبال کنید. اگر سوالی دارید یا نیاز به تحلیل داده دارید، با کارشناسان ما تماس بگیرید!

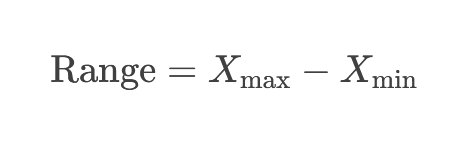 مثال کاربردی
مثال کاربردی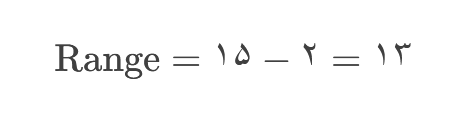 مزایا و محدودیتها
مزایا و محدودیتها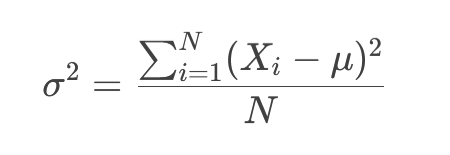 واریانس نمونه:
واریانس نمونه: مثال محاسبه
مثال محاسبه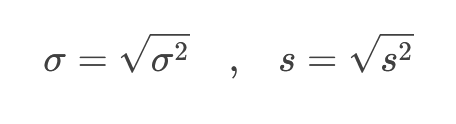 مثال
مثال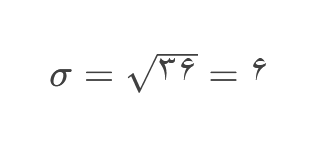 کاربردهای انحراف معیار
کاربردهای انحراف معیار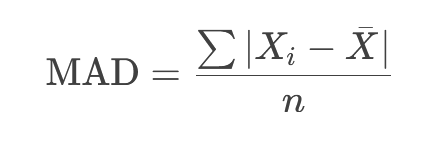 مثال
مثال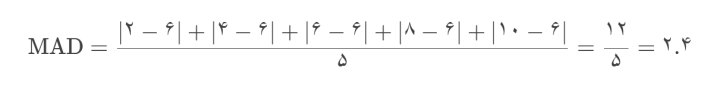 مزیت کلیدی
مزیت کلیدی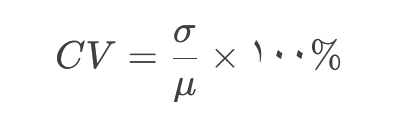 مثال کاربردی
مثال کاربردی
ممنون از زحماتتون