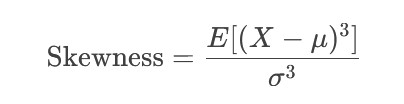کشیدگی و چولگی در آمار: مفاهیم، کاربردها و روشهای تشخیص
مقدمه
در دنیای آمار و تحلیل دادهها، کشیدگی (Kurtosis) و چولگی (Skewness) دو مفهوم اساسی هستند که به بررسی توزیع دادهها میپردازند. این دو شاخص بهطور دقیقتر شکل توزیع را نسبت به توزیع نرمال استاندارد توصیف میکنند و در تحلیلهای آماری، مدلسازی دادهها و حتی تصمیمگیریهای تجاری نقش حیاتی ایفا میکنند. در این مقاله، بهصورت جامع و مفصل به تعریف کشیدگی و چولگی، انواع آنها، روشهای محاسبه و کاربردهای عملی آنها میپردازیم. همچنین، تأثیر این مفاهیم در تحلیلهای آماری و نحوه تفسیر آنها را بررسی خواهیم کرد.
چولگی (Skewness) چیست؟
چولگی معیاری است که میزان عدم تقارن توزیع دادهها را نسبت به منحنی نرمال نشان میدهد. در یک توزیع کاملاً متقارن (مانند توزیع نرمال)، چولگی صفر است. اما اگر دادهها به یک سمت متمایل باشند، چولگی مثبت یا منفی خواهد بود.
انواع چولگی
چولگی مثبت (Right-Skewed):
زمانی اتفاق میافتد که دم توزیع به سمت راست کشیده شده باشد.
میانگین > میانه > مُد
مثال: توزیع درآمد در جامعه (اکثر افراد درآمد متوسط دارند، اما تعداد کمی درآمد بسیار بالا دارند).
چولگی منفی (Left-Skewed):
زمانی رخ میدهد که دم توزیع به سمت چپ کشیده شده باشد.
میانگین < میانه < مُد
مثال: نمرات یک امتحان آسان (اکثر دانشآموزان نمره بالا میگیرند و تعداد کمی نمره پایین دارند).
محاسبه چولگی
فرمول محاسبه چولگی به صورت زیر است:
 : دادهها
: دادهها: میانگین
: انحراف معیار
: امید ریاضی
اگر مقدار چولگی بین -0.5 تا 0.5 باشد، توزیع تقریباً متقارن است. مقادیر خارج از این بازه نشاندهنده چولگی قابل توجه هستند.
کشیدگی (Kurtosis) چیست؟
کشیدگی معیاری است که ضخامت دمهای توزیع و میزان تمرکز دادهها را حول میانگین نشان میدهد. این مفهوم به ما میگوید که آیا دادهها دارای outlierهای (نقاط پرت) زیاد هستند یا خیر.
انواع کشیدگی
کشیدگی نرمال (Mesokurtic):
مقدار کشیدگی نزدیک به صفر است (معمولاً برابر با ۳ در برخی تعاریف).
مشابه توزیع نرمال است.
کشیدگی مثبت (Leptokurtic):
کشیدگی بیشتر از نرمال (معمولاً > ۳).
دمهای سنگینتر و قله باریکتر.
احتمال وجود outlierها بیشتر است.
مثال: بازدهی سهام پرریسک.
کشیدگی منفی (Platykurtic):
کشیدگی کمتر از نرمال (معمولاً < ۳).
دمهای سبکتر و قله پهنتر.
دادهها پراکندهتر هستند.
مثال: توزیع قد افراد در یک جامعه بزرگ.
محاسبه کشیدگی
فرمول کشیدگی به صورت زیر است:
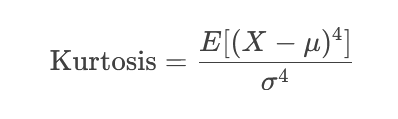 در برخی منابع، مقدار کشیدگی نرمال را ۳ در نظر میگیرند و از کشیدگی تعدیلشده (Excess Kurtosis) استفاده میکنند:
در برخی منابع، مقدار کشیدگی نرمال را ۳ در نظر میگیرند و از کشیدگی تعدیلشده (Excess Kurtosis) استفاده میکنند:
Excess Kurtosis=Kurtosis−3
کشیدگی بالا Excess Kurtosis > 0 → Leptokurtic
کشیدگی پایین Excess Kurtosis < 0 → Platykurtic
تفاوت چولگی و کشیدگی
| مفهوم | چولگی (Skewness) | کشیدگی (Kurtosis) |
|---|---|---|
| تعریف | میزان عدم تقارن توزیع | ضخامت دمهای توزیع |
| مقدار صفر | توزیع متقارن | توزیع نرمال (در برخی تعاریف ۳) |
| مقادیر مثبت | دم سمت راست بلندتر | دمهای سنگینتر (Leptokurtic) |
| مقادیر منفی | دم سمت چپ بلندتر | دمهای سبکتر (Platykurtic) |
کاربردهای چولگی و کشیدگی در تحلیل داده
تجزیه و تحلیل مالی:
در بازار سهام، توزیع بازدهی اغلب چوله است و کشیدگی بالایی دارد. این موضوع در مدیریت ریسک مهم است.
کنترل کیفیت:
در صنعت، بررسی چولگی و کشیدگی دادههای تولید به شناسایی انحرافات کمک میکند.
تحقیقات پزشکی:
توزیع دادههای پزشکی (مانند فشار خون) ممکن است چوله باشد و نیاز به تبدیل داده داشته باشد.
یادگیری ماشین:
برخی الگوریتمها (مانند SVM و رگرسیون خطی) به نرمال بودن دادهها حساس هستند. بررسی چولگی و کشیدگی به پیشپردازش داده کمک میکند.
نحوه تفسیر چولگی و کشیدگی در نرمافزار spss
در نرمافزارهایی مانند SPSS، R و Python میتوان این مقادیر را محاسبه کرد.
- در SPSS:
از مسیر Analyze > Descriptive Statistics > Descriptives و انتخاب گزینه Skewness و Kurtosis. - برای یادگیری بیشتر در این زمینه با مثال های کاربردی و مطالعه روش تجزیه و تحلیل خروجی نرم افزار کتاب “آموزش spss از مبتدی تا پیشرفته” را مطالعه کنید.
جمعبندی
چولگی و کشیدگی دو شاخص کلیدی در آمار هستند که به تحلیل شکل توزیع دادهها کمک میکنند. چولگی میزان عدم تقارن و کشیدگی میزان تمرکز دادهها در دمها را نشان میدهد. این مفاهیم در حوزههای مختلفی مانند مالی، پزشکی و یادگیری ماشین کاربرد دارند. با استفاده از نرمافزارهای آماری میتوان این مقادیر را محاسبه و تفسیر کرد. درک صحیح این مفاهیم به تحلیل دقیقتر دادهها و تصمیمگیری بهتر منجر میشود.
سوالات متداول (FAQ)
چرا کشیدگی مهم است؟
زیرا وجود outlierها و شدت پراکندگی دادهها را نشان میدهد.اگر دادهها چوله باشند چه کنیم؟
میتوان از تبدیلهای مانند لگاریتم یا Box-Cox برای متقارنسازی استفاده کرد.آیا توزیع نرمال همیشه چولگی صفر دارد؟
بله، توزیع نرمال کاملاً متقارن است و چولگی آن صفر است.کشیدگی منفی به چه معناست؟
یعنی دادهها پراکندهتر از توزیع نرمال هستند