ضریب تغییرات (CV): جامع‌ترین راهنمای کاربردی و تحلیلی

مقدمه: معرفی ضریب تغییرات و اهمیت آن در آمار

ضریب تغییرات (Coefficient of Variation) که به اختصار CV نامیده می‌شود، یکی از معیارهای نسبی پراکندگی است که به طور گسترده در علوم آماری مورد استفاده قرار می‌گیرد. این شاخص آماری قدرت مقایسه پراکندگی داده‌ها را در شرایطی که واحدهای اندازه‌گیری مختلف هستند یا میانگین‌های متفاوتی دارند، فراهم می‌کند. برخلاف معیارهای مطلق پراکندگی مانند انحراف معیار، ضریب تغییرات یک شاخص بدون واحد است که امکان مقایسه‌های معنادار بین مجموعه داده‌های کاملاً متفاوت را ممکن می‌سازد.

در دنیای واقعی، پژوهشگران و تحلیلگران داده اغلب با موقعیت‌هایی مواجه می‌شوند که نیاز به مقایسه تغییرپذیری دو یا چند مجموعه داده با واحدهای اندازه‌گیری مختلف دارند. به عنوان مثال، ممکن است بخواهیم تغییرپذیری درآمد ماهانه کارمندان یک شرکت (بر حسب میلیون تومان) را با تغییرپذیری قد آن‌ها (بر حسب سانتیمتر) مقایسه کنیم. در چنین مواردی، معیارهای مطلق پراکندگی مانند واریانس یا انحراف معیار قابل استفاده نیستند، اما ضریب تغییرات به عنوان یک ناجی ظاهر می‌شود.

تعریف ریاضی و فرمول محاسبه ضریب تغییرات

ضریب تغییرات به صورت نسبت انحراف معیار به میانگین تعریف می‌شود و معمولاً به صورت درصد بیان می‌گردد. فرمول ریاضی آن به شرح زیر است:

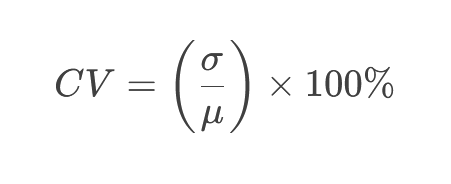که در این فرمول:

• σ (سیگما) نماد انحراف معیار جامعه آماری

• μ (مو) نماد میانگین جامعه آماری است.

در مواردی که با نمونه‌های آماری سر و کار داریم، فرمول به این صورت تعدیل می‌شود:

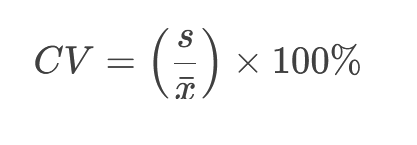که در آن:

• s انحراف معیار نمونه

• x̄ میانگین نمونه است.

مثال محاسبه عملی

فرض کنید دو مجموعه داده داریم:

1. مجموعه A: میانگین = 50، انحراف معیار = 5

2. مجموعه B: میانگین = 200، انحراف معیار = 20

محاسبه ضریب تغییرات برای هر مجموعه:

• CV_A = (5/50)×100% = 10%

• CV_B = (20/200)×100% = 10%

این نتیجه نشان می‌دهد که نسبت پراکندگی به میانگین در هر دو مجموعه داده یکسان است، اگرچه مقیاس اندازه‌گیری آنها کاملاً متفاوت است.

مزایای استفاده از ضریب تغییرات در تحلیل داده‌ها

1. قابلیت مقایسه مجموعه داده‌های با واحدهای مختلف

بزرگترین مزیت ضریب تغییرات امکان مقایسه پراکندگی مجموعه داده‌هایی است که در واحدهای اندازه‌گیری متفاوتی بیان شده‌اند. این ویژگی در پژوهش‌های بین‌رشته‌ای و مطالعاتی که متغیرهای ناهمگن دارند، بسیار ارزشمند است.

2. عدم وابستگی به مقیاس اندازه‌گیری

از آنجا که CV یک مقدار نسبی و بدون بعد است، تحت تأثیر تغییر مقیاس داده‌ها (مثلاً تبدیل از سانتیمتر به متر) قرار نمی‌گیرد. این خاصیت باعث می‌شود در مطالعات طولی که ممکن است واحد اندازه‌گیری تغییر کند، همچنان قابل استناد باشد.

3. ابزاری مناسب برای ارزیابی ثبات و پایایی

در کنترل کیفیت و مطالعات تولیدی، ضریب تغییرات معیار مناسبی برای سنجش ثبات فرآیندهاست. هرچه CV کوچکتر باشد، نشان‌دهنده ثبات بیشتر سیستم است.

محدودیت‌ها و موارد عدم کاربرد ضریب تغییرات

1. عدم مناسب بودن برای داده‌های با میانگین نزدیک به صفر

وقتی میانگین داده‌ها به صفر نزدیک باشد، مقدار CV به سمت بی‌نهایت میل می‌کند که تفسیر آن مشکل‌ساز خواهد بود. در چنین مواردی استفاده از معیارهای مطلق پراکندگی مناسب‌تر است.

2. حساسیت به مقیاس نسبت

ضریب تغییرات برای داده‌هایی که در مقیاس نسبی (ratio scale) اندازه‌گیری شده‌اند مناسب است، اما برای داده‌های در مقیاس فاصله‌ای (interval scale) که صفر مطلق ندارند، قابل استفاده نیست.

3. تأثیرپذیری از توزیع داده‌ها

CV برای توزیع‌های متقارن و نرمال بهترین عملکرد را دارد. در توزیع‌های بسیار چوله (skewed) ممکن است گمراه‌کننده باشد.

کاربردهای عملی ضریب تغییرات در صنعت و پژوهش

1. کنترل کیفیت و مهندسی صنایع

در صنعت تولید، از CV برای ارزیابی یکنواختی محصولات استفاده می‌شود. به عنوان مثال، در تولید پیچ و مهره، ضریب تغییرات قطر محصولات نشان‌دهنده میزان دقت دستگاه‌های تولیدی است.

2. مطالعات اقتصادی و مالی

در اقتصاد، از CV برای مقایسه ریسک سرمایه‌گذاری در بازارهای مختلف استفاده می‌شود. هرچه CV بازدهی یک دارایی بیشتر باشد، نشان‌دهنده نوسانات بیشتر و در نتیجه ریسک بالاتر است.

3. پژوهش‌های پزشکی و بیولوژیکی

در مطالعات بالینی، CV برای مقایسه تغییرپذیری پارامترهای بیولوژیک مانند سطح قند خون یا فشار خون در جمعیت‌های مختلف به کار می‌رود.

تفسیر مقادیر ضریب تغییرات

راهنمای کلی برای تفسیر CV:

• CV < 10%: تغییرپذیری کم (عالی)

• 10% ≤ CV ≤ 20%: تغییرپذیری متوسط (قابل قبول)

• CV > 20%: تغییرپذیری بالا (نیاز به بررسی)

البته این بازه‌ها در رشته‌های مختلف ممکن است متفاوت باشد. به عنوان مثال در مطالعات بیولوژیکی، حتی CVهای کمتر از 50% نیز ممکن است قابل قبول تلقی شوند.

مقایسه ضریب تغییرات با سایر معیارهای پراکندگی

تفاوت CV با انحراف معیار:

در حالی که انحراف معیار یک شاخص مطلق است و فقط برای داده‌های با واحد یکسان قابل مقایسه است، CV یک شاخص نسبی است که امکان مقایسه بین مجموعه داده‌های کاملاً متفاوت را فراهم می‌کند.

مقایسه CV با دامنه تغییرات:

دامنه تغییرات فقط از دو نقطه حدی استفاده می‌کند، در حالی که CV از تمام داده‌ها در محاسبه انحراف معیار استفاده می‌نماید و بنابراین معیار کامل‌تری است.

محاسبه ضریب تغییرات در نرم‌افزارهای آماری

نحوه محاسبه در Excel:

1. محاسبه میانگین با تابع AVERAGE

2. محاسبه انحراف معیار با تابع STDEV.P (برای جامعه) یا STDEV.S (برای نمونه)

3. تقسیم انحراف معیار بر میانگین و ضرب در 100

محاسبه در R:

cv <- function(x) {sd(x)/mean(x)*100}
cv(data_vector)

محاسبه در SPSS:

از مسیر Analyze > Descriptive Statistics > Descriptives و انتخاب گزینه Coefficient of variation.

مطالعات موردی واقعی با استفاده از ضریب تغییرات

مطالعه 1: مقایسه ثبات تولید در دو کارخانه

در پژوهشی که به مقایسه کیفیت تولید دو کارخانه پرداخته بود، CV برای کارخانه A برابر 8% و برای کارخانه B برابر 15% محاسبه شد. این نتیجه نشان داد که فرآیندهای تولیدی کارخانه A از ثبات بیشتری برخوردارند.

مطالعه 2: ارزیابی ریسک سرمایه‌گذاری

در تحلیل بازارهای مالی، CV بازدهی ماهانه سهام شرکت X برابر 25% و شرکت Y برابر 40% بود که نشان می‌داد سرمایه‌گذاری در شرکت X با نوسانات کمتری همراه است.

نکات کلیدی برای استفاده صحیح از ضریب تغییرات

1. همیشه واحد اندازه‌گیری را در گزارش ذکر کنید، اگرچه CV خود بدون واحد است.

2. برای داده‌های چوله، استفاده از میانه به جای میانگین ممکن است مناسب‌تر باشد.

3. در گزارش‌دهی، دقت کنید که آیا از انحراف معیار جامعه یا نمونه استفاده کرده‌اید.

4. از CV برای مقایسه‌های درون‌گروهی استفاده کنید نه به عنوان یک معیار مطلق.

نتیجه‌گیری: جایگاه ضریب تغییرات در تحلیل داده‌های مدرن

ضریب تغییرات به عنوان یک ابزار قدرتمند در تحلیل‌های آماری، امکان مقایسه‌های معنادار بین مجموعه داده‌های ناهمگن را فراهم می‌کند. این شاخص به ویژه در عصر داده‌های بزرگ (Big Data) که اغلب با متغیرهای مختلف و ناهمگن سروکار داریم، اهمیت دوچندانی یافته است. با این حال، مانند هر ابزار آماری دیگری، شناخت محدودیت‌ها و شرایط صحیح کاربرد آن ضروری است.

تسلط بر محاسبه و تفسیر ضریب تغییرات می‌تواند دیدگاه‌های ارزشمندی در پژوهش‌های علمی، تصمیم‌گیری‌های مدیریتی و تحلیل‌های اقتصادی در اختیار محققان قرار دهد. با ترکیب این شاخص با دیگر معیارهای آماری، می‌توان به درک جامع‌تری از رفتار داده‌ها دست یافت.