تحلیل همبستگی در پژوهش: راهنمای جامع و کاربردی

مقدمه: اهمیت تحلیل همبستگی در تحقیقات

تحلیل همبستگی یکی از روش‌های اساسی در آمار و پژوهش‌های علمی است که به بررسی روابط بین متغیرها می‌پردازد. این روش به محققان کمک می‌کند تا شدت و جهت ارتباط بین دو یا چند متغیر را اندازه‌گیری کنند. در این مقاله به بررسی انواع ضریب همبستگی، کاربردهای آن و نحوه تفسیر نتایج می‌پردازیم.

شاخص‌های رابطه بین متغیرها

برای توصیف روابط بین متغیرها با توجه به سطح اندازه‌گیری آن‌ها، شاخص‌های مختلفی وجود دارد. یک شاخص رابطه عددی است که قدرت ارتباط بین متغیرها را نشان می‌دهد.

🔍 تحلیل همبستگی چیست؟

تحلیل همبستگی روشی آماری برای سنجش شدت رابطه خطی بین دو متغیر است. اولین گام در بررسی رابطه دو متغیر، رسم نمودار پراکنش (Scatter Plot) است. این نمودار به ما کمک می‌کند تا الگوی احتمالی بین داده‌ها را شناسایی کنیم.

📌 نکته کلیدی:

• اگر نقاط داده‌ها حول یک خط راست جمع شده باشند، می‌توان از ضریب همبستگی برای اندازه‌گیری رابطه استفاده کرد.

• ضریب همبستگی یک شاخص بدون واحد است و تفسیر آن آسان است.

انواع ضرایب همبستگی

با توجه به سطح اندازه‌گیری متغیرها، از ضرایب همبستگی مختلف استفاده می‌شود. دو مورد از مهم‌ترین آن‌ها عبارتند از:

1️⃣ ضریب همبستگی پیرسون (Pearson)

• کاربرد: اندازه‌گیری رابطه خطی بین دو متغیر فاصله‌ای یا نسبتی.

• محدوده مقادیر: بین 1- تا 1+

  • 1+: رابطه خطی مثبت کامل

  • 1-: رابطه خطی منفی کامل

  • 0: عدم وجود رابطه خطی

📢 نکات مهم پیرسون:
✅ قرینه است (نقش متغیر مستقل و وابسته تأثیری ندارد).
❌ همبستگی ≠ علیت (وجود رابطه لزوماً به معنای تأثیر علّی نیست).
❌ ضریب صفر فقط عدم رابطه خطی را نشان می‌دهد، نه عدم وجود هرگونه رابطه (ممکن است رابطه غیرخطی وجود داشته باشد).

📝 فرمول ضریب همبستگی پیرسون:

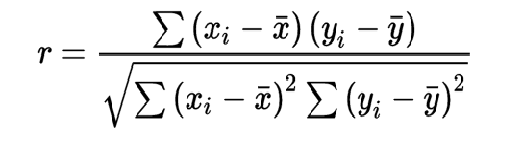
r: ضریب همبستگی

x_i: مشاهدات متغیر x

y_i: مشاهدات متغیر y

x̄: میانگین مشاهدات متغیر x

ȳ: میانگین مشاهدات متغیر y

2️⃣ ضریب همبستگی اسپیرمن (Spearman)

• کاربرد: برای داده‌های رتبه‌ای یا زمانی که فرض نرمال بودن داده‌ها برقرار نیست.

• محاسبه: مانند پیرسون، اما بر اساس رتبه داده‌ها.

📝 فرمول ضریب همبستگی اسپیرمن:

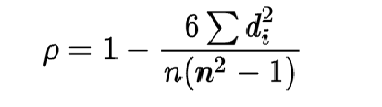ƿ: ضریب همبستگی رتبه ای اسپیرمن

d_i: تفاوت بین رتبه هر جفت مشاهده

n: تعداد مشاهدات

نحوه محاسبه ضریب همبستگی

🔹 محاسبه دستی: برای نمونه‌های کوچک با استفاده از فرمول‌های بالا.
🔹 نرم‌افزارهای آماری: مانند SPSS، Excel، R و Python برای داده‌های حجیم.
📚 پیشنهاد: کتاب “آموزش SPSS از مبتدی تا پیشرفته” برای یادگیری تحلیل‌های همبستگی.

کاربردهای تحلیل همبستگی

✔ بررسی رابطه درآمد و سطح تحصیلات
✔ سنجش ارتباط بیکاری و نرخ جرم
✔ تحلیل رابطه مصرف دارو و بهبود بیماری
✔ شناسایی الگوهای بازارهای مالی

⚠ هشدار: همیشه به خاطر داشته باشید که “همبستگی به معنای علیت نیست”!

نتیجه‌گیری

تحلیل همبستگی ابزاری قدرتمند برای شناسایی روابط بین متغیرهاست، اما تفسیر آن نیازمند دقت است. انتخاب بین پیرسون و اسپیرمن به سطح داده‌ها بستگی دارد و استفاده از نرم‌افزارهای آماری محاسبات را تسهیل می‌کند.

📌 سؤالات متداول (FAQ):
🔸 تفاوت همبستگی و رگرسیون چیست؟

• همبستگی شدت رابطه را می‌سنجد، اما رگرسیون برای پیش‌بینی استفاده می‌شود.
  🔸 آیا ضریب همبستگی 0.5 قابل قبول است؟

• بستگی به حوزه تحقیق دارد، اما معمولاً مقادیر بالای 0.7 قوی در نظر گرفته می‌شوند.