تحلیل همبستگی در پژوهش

شاخص های رابطه متفاوت و زیادی برای توصیف روابط بین متغیرها با توجه به سطح اندازه گیری متغیرهای مورد مطالعه وجود دارد. یک شاخص رابطه، عددی است که مقدار آن نشانگر قدرت رابطه متغیرهاست.

یکی از روش های آماری برای بررسی و شناخت روابط بین متغیرها، تحلیل همبستگی است. در تحلیل همبستگی هدف بیان شدت رابطه خطی بین دو متغیر است.

اولین گام در بررسی رابطه دو متغیر رسم نمودار پراکنش داده هاست. با مشاهده نمودار پراکنش می توان پی برد که آیا الگویی بین مقادیر مشاهده شده وجود دارد یا اینکه نقاط به صورت تصادفی پخش شده اند.

اگر نقاط روی یک نمودار اطراف یک خط راست جمع شده باشند، رابطه بین آنها را می توان با ضریب همبستگی اندازه گرفت.

ضریب همبستگی شاخصی است که مقدار آن به واحدهای اندازه گیری مرتبط نیست و به راحتی قابل تفسیر است.

با توجه به سطح اندازه گیری متغیرها ضرایب همبستگی متفاوت خواهند بود. از مهمترین ضرایب همبستگی می توان به ضریب همبستگی پیرسون و اسپیرمن اشاره کرد.

ضریب همبستگی پیرسون

ضریب همبستگی پیرسون برای نشان دادن جهت و شدت رابطه خطی متغیرهایی که در سطح فاصله ای اندازه گیری شده اند به کار می رود. این شاخص برای متغیرهای ترتیبی و اسمی کاربرد و مفهوم ندارد.

مقدار ضریب همبستگی پیرسون در دامنه 1- تا 1+ قرار می گیرد. اگر تمام نقاط روی خطی با شیب مثبت قرار داشته باشند مقدار ضریب همبستگی برابر 1+ و اگر همه نقاط بر روی خطی با شیب منفی قرار بگیرند مقدار ضریب همبستگی برابر 1- خواهد بود.

مقدار ضریب همبستگی صفر نشان می دهد که هیچ گونه رابطه خطی بین دو متغیر وجود ندارد. هر چه مقدار قدرمطلق ضریب همبستگی به 1 نزدیک تر باشد، رابطه خطی قوی تری بین دو متغیر بیان می شود.

ضریب همبستگی شاخصی قرینه است و صرفنظر از اینکه کدام متغیر مستقل و کدام وابسته است نتیجه یکسانی بدست می دهد. بنابراین ضریب همبستگی علیت را بیان نمی کند و وجود یک همبستگی بین دو متغیر همیشه نشان نمی دهد که یکی از متغیرها علت دیگری است.

ضریب همبستگی صفر نشان دهنده عدم وجود رابطه خطی است و نه صرفاً عدم وجود هر نوع رابطه ای. مثلاً ممکن است دو متغیر با ضریب همبستگی صفر رابطه قوی غیر خطی (منحنی) با هم داشته باشند.

یکی از مهمترین کاربردهای ضریب همبستگی در تحلیل رگرسیون خطی است. زیرا تنها زمانی محاسبه معادله رگرسیون خطی موجه است که رابطه بین متغیر وابسته و متغیر(مستقل) رابطه ای خطی باشد.

فرمول ضریب همبستگی پیرسون

برای دو متغیر x و y ضریب همبستگی با فرمول زیر محاسبه می شود:

 

 

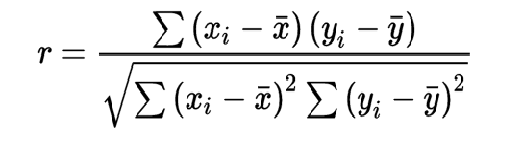
r: ضریب همبستگی

x_i: مشاهدات متغیر x

y_i: مشاهدات متغیر y

x̄: میانگین مشاهدات متغیر x

ȳ: میانگین مشاهدات متغیر y

ضریب همبستگی اسپیرمن

این ضریب همبستگی همان ضریب همبستگی پیرسون است که برای داده های رتبه بندی شده به کار برده می شود. اگر داده ها فاصله ای باشند در محاسبه ضریب همبستگی اسپیرمن از رتبه داده ها استفاده می شود.

فرمول ضریب همبستگی اسپیرمن

برای دو متغیر رتبه ای x و y ضریب همبستگی با فرمول زیر محاسبه می شود:

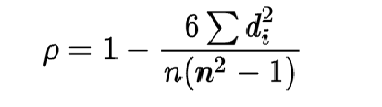ƿ: ضریب همبستگی رتبه ای اسپیرمن

d_i: تفاوت بین رتبه هر جفت مشاهده

n: تعداد مشاهدات

محاسبه ضریب همبستگی:

با توجه به پیچیدگی فرمول ضریب همبستگی، در مواقعی که تعداد داده ها زیاد است محاسبه دستی آن خسته کننده است. با استفاده از نرم افزارهای آماری یا صفحات گسترده مانند اکسل می توان ضریب همبستگی را به راحتی محاسبه کرد. از جمله نرم افزارهای آماری که می توان برای محاسبه ضریب همبستگی استفاده کرد نرم افزار spss است. با مطالعه کتاب ” آموزش spss از مبتدی تا پیشرفته” می توانید به راحتی نحوه محاسبه انواع ضریب همبستگی و سایر شاخص های رابطه را بیاموزید و نحوه تفسیر آن ها را فرا گیرید.

کاربرد تحلیل های همبستگی:

تحلیل های همبستگی از آن جهت سودمند هستند که می توانند چگونگی ارتباط و روندها یا الگوهای مختلف بین متغیرهای مختلف را مشخص کنند. مثلاً با استفاده از تحلیل همبستگی می توان شدت رابطه میزان درآمد با سطح تحصیلات یا همبستگی بیکاری و جرم را مورد بررسی قرار داد.

تحلیل همبستگی به ما اجازه می‌دهد با اطمینان بگوییم که رابطه‌ای بین دو الگو یا متغیر متفاوت وجود دارد یا نه.

مهم است به این نکته توجه شود که همبستگی با علّیت یکسان نیست، بنابراین در حالی که یک همبستگی قوی بین تحصیلات و میزان طلاق وجود دارد، این بدان معنا نیست که کاهش طلاق در میان زنان به دلیل میزان تحصیلات است.