متغیر تصادفی در آمار: مفاهیم، انواع و کاربردها

مقدمه: درک مفهوم متغیر تصادفی

در دنیای آمار و احتمال، متغیر تصادفی (Random Variable) یکی از اساسی ترین و پرکاربردترین مفاهیم است که پایه بسیاری از تحلیل های آماری را تشکیل می دهد. یک متغیر تصادفی در واقع تابعی است که هر نتیجه ممکن از یک آزمایش تصادفی را به یک مقدار عددی نسبت می دهد. به بیان ساده تر، متغیر تصادفی راهی برای کمی کردن نتایج غیرقطعی و تصادفی است که در پدیده های مختلف مشاهده می کنیم. اهمیت این مفهوم در آمار به حدی است که بدون درک صحیح آن، نمی توان بسیاری از روش های پیشرفته تحلیل داده را فهمید یا به کار برد. در این مقاله جامع، به بررسی عمیق متغیرهای تصادفی، انواع آن ها، ویژگی ها، توزیع های احتمال مرتبط و کاربردهای عملی آنها در تحلیل های آماری می پردازیم.

تعریف دقیق متغیر تصادفی از دیدگاه ریاضی

از دیدگاه ریاضی دقیق، یک متغیر تصادفی تابعی قابل اندازه گیری از فضای نمونه (Sample Space) یک آزمایش تصادفی به اعداد حقیقی است. به عبارت فنی تر، اگر Ω فضای نمونه یک آزمایش تصادفی باشد، آنگاه متغیر تصادفی X تابعی است به صورت X:Ω→ℝ که برای هر بازه واقعی I، مجموعه {ω∈Ω | X(ω)∈I} یک رویداد است. این تعریف انتزاعی در نگاه اول ممکن است پیچیده به نظر برسد، اما در عمل بسیار شهودی است. برای مثال، در پرتاب یک سکه، فضای نمونه ما شامل دو نتیجه “شیر” و “خط” است. میتوانیم متغیر تصادفی X را به این صورت تعریف کنیم که به نتیجه شیر مقدار 1 و به نتیجه خط مقدار 0 نسبت دهد. به این ترتیب، پدیده تصادفی پرتاب سکه را به اعداد ترجمه کرده ایم که تحلیل ریاضی آن ساده تر است.

انواع متغیرهای تصادفی: گسسته در مقابل پیوسته

متغیرهای تصادفی به دو دسته اصلی تقسیم می شوند: گسسته و پیوسته. این تقسیم بندی بر اساس نوع مقادیری است که متغیر تصادفی می تواند بگیرد و نحوه توصیف رفتار احتمالی آن.

متغیرهای تصادفی گسسته

یک متغیر تصادفی گسسته متغیری است که مجموعه مقادیر ممکن آن یا متناهی است یا بی نهایت اما شمارش پذیر. به عبارت دیگر، میتوانیم تمام مقادیر ممکن متغیر را لیست کنیم (حتی اگر این لیست بی نهایت باشد). مثال های متداول شامل تعداد دفعات شیر آمدن در 10 پرتاب سکه، تعداد مشتریان وارد شده به یک فروشگاه در یک ساعت، یا تعداد خطاهای یک سیستم کامپیوتری در یک روز هستند. برای توصیف رفتار احتمالی یک متغیر گسسته از تابع جرم احتمال (PMF) استفاده می کنیم که به هر مقدار ممکن متغیر، احتمال وقوع آن را نسبت می دهد.

متغیرهای تصادفی پیوسته

در مقابل، متغیر تصادفی پیوسته متغیری است که مقادیر آن می تواند هر عددی در یک بازه پیوسته از اعداد حقیقی باشد (بی نهایت ناشمارا). مثال های رایج شامل قد افراد در یک جامعه، زمان بین دو رویداد متوالی، یا دما در یک نقطه خاص هستند. برای متغیرهای پیوسته، احتمال گرفتن هر مقدار خاص دقیق صفر است (زیرا بینهایت مقدار ممکن وجود دارد)، بنابراین به جای تابع جرم احتمال، از تابع چگالی احتمال (PDF) استفاده می کنیم که احتمال را روی بازه های مختلف تعریف میکند. احتمال اینکه متغیر در بازه خاصی قرار گیرد برابر است با انتگرال تابع چگالی روی آن بازه.

توزیع احتمال و توصیف رفتار متغیرهای تصادفی

هر متغیر تصادفی با توزیع احتمال آن به طور کامل مشخص می شود. توزیع احتمال در واقع توصیفی ریاضی از رفتار احتمالی متغیر است که نشان می دهد چه مقادیری با چه احتمالاتی رخ می دهند. برای متغیرهای گسسته، این توصیف معمولاً از طریق تابع جرم احتمال (PMF) انجام می شود که به صورت p(x)=P(X=x) تعریف می شود. برای متغیرهای پیوسته، تابع چگالی احتمال (PDF) که معمولاً با f(x) نشان داده می شود این نقش را ایفا می کند. علاوه بر این، تابع توزیع تجمعی (CDF) که به صورت F(x)=P(X≤x) تعریف می شود، هم برای متغیرهای گسسته و هم پیوسته کاربرد دارد و احتمال اینکه متغیر مقداری کمتر یا مساوی x بگیرد را نشان می دهد.

ویژگیهای مهم توزیع های احتمال

توزیع های احتمال مختلف دارای ویژگی های منحصر به فردی هستند که آنها را برای مدلسازی پدیده های خاص مناسب می سازد. برخی از این ویژگی های کلیدی شامل:

1. امید ریاضی (Expected Value): میانگین وزنی مقادیر ممکن متغیر که نشان دهنده مرکز توزیع است.

2. واریانس (Variance): معیاری از پراکندگی مقادیر حول میانگین که با Var(X) یا σ² نشان داده می شود.

3. چولگی (Skewness): میزان عدم تقارن توزیع حول میانگین.

4. کشیدگی (Kurtosis): معیاری از سنگینی دم های توزیع.

این ویژگی ها به ما کمک می کنند تا رفتار متغیرهای تصادفی را خلاصه و مقایسه کنیم.

متغیرهای تصادفی چندبعدی و توزیع های مشترک

در بسیاری از موقعیت های واقعی، با چندین متغیر تصادفی به طور همزمان سروکار داریم که ممکن است با هم در ارتباط باشند. این منجر به مفهوم متغیرهای تصادفی چندبعدی و توزیع های احتمال مشترک می شود. برای دو متغیر تصادفی X و Y، توزیع مشترک آنها رفتار همزمان این دو متغیر را توصیف می کند. در حالت گسسته، تابع جرم احتمال مشترک به صورت p(x,y)=P(X=x,Y=y) تعریف می شود و در حالت پیوسته، تابع چگالی مشترک f(x,y) داریم. از توزیع های مشترک می توان برای به دست آوردن توزیع های حاشیه ای (توزیع هر متغیر به تنهایی) و توزیع های شرطی (توزیع یک متغیر با فرض مقدار مشخصی برای متغیر دیگر) استفاده کرد.

کوواریانس و همبستگی

دو مفهوم مهم در بررسی روابط بین متغیرهای تصادفی، کوواریانس و ضریب همبستگی هستند. کوواریانس معیاری از جهت و میزان تغییرات همزمان دو متغیر است:

Cov(X,Y) = E[(X-E[X])(Y-E[Y])]

ضریب همبستگی که معمولاً با ρ نشان داده می شود، نسخه نرمال شده کوواریانس است و مقداری بین -1 و 1 دارد که شدت و جهت رابطه خطی بین متغیرها را نشان می دهد.

متغیرهای تصادفی مستقل و خواص آنها

دو متغیر تصادفی X و Y را مستقل می گوییم اگر توزیع مشترک آنها برابر حاصلضرب توزیع های حاشیگی باشد. به عبارت دیگر، برای همه مقادیر x و y داشته باشیم:

P(X=x,Y=y) = P(X=x)P(Y=y) (در حالت گسسته)
f(x,y) = f_X(x)f_Y(y) (در حالت پیوسته)

متغیرهای مستقل خواص جالبی دارند. برای مثال، امید ریاضی حاصلضرب آنها برابر حاصلضرب امیدهای ریاضیشان است (E[XY]=E[X]E[Y]) و واریانس جمع آنها برابر جمع واریانس هایشان است (Var(X+Y)=Var(X)+Var(Y)). این خواص محاسبات را در بسیاری از مسائل آماری ساده می کنند.

تبدیل متغیرهای تصادفی و توزیع توابع آنها

در عمل، اغلب با توابعی از متغیرهای تصادفی سروکار داریم. برای مثال، اگر X یک متغیر تصادفی باشد، ممکن است بخواهیم توزیع Y=g(X) را برای برخی توابع g پیدا کنیم. روشهای مختلفی برای این کار وجود دارد که بستگی به نوع متغیر (گسسته یا پیوسته) و ماهیت تابع g دارد. برای متغیرهای گسسته، معمولاً میتوانیم مقادیر ممکن Y را پیدا کرده و احتمالات مربوطه را جمع بزنیم. برای متغیرهای پیوسته، اگر تابع g یکبهیک باشد، میتوانیم از روش تغییر متغیر استفاده کنیم. در موارد پیچیدهتر، ممکن است نیاز به استفاده از تکنیکهای پیشرفتهتری مانند تابع مولد گشتاور یا شانون مستقیم باشد.

امید ریاضی و گشتاورهای متغیرهای تصادفی

امید ریاضی (Expected Value) یکی از مهمترین مفاهیم در نظریه احتمال است که میانگین وزنی مقادیر ممکن یک متغیر تصادفی را با وزن های برابر با احتمالات آنها نشان می دهد. برای متغیر گسسته، امید ریاضی به صورت E[X]=∑x_ip(x_i) و برای متغیر پیوسته به صورت E[X]=∫xf(x)dx تعریف می شود. امید ریاضی خواص خطی دارد: E[aX+bY+c]=aE[X]+bE[Y]+c برای هر ثابت a,b,c.

گشتاورهای یک متغیر تصادفی تعمیم هایی از مفهوم امید ریاضی هستند. گشتاور مرتبه k حول مبدأ به صورت μ’_k=E[X^k] و گشتاور مرتبه k حول میانگین به صورت μ_k=E[(X-μ)^k] تعریف می شود که در آن μ=E[X]. گشتاورهای اول و دوم حول مبدأ به ترتیب برابر میانگین و E[X²] هستند. گشتاور دوم حول میانگین همان واریانس متغیر تصادفی است. گشتاورهای بالاتر اطلاعاتی درباره شکل توزیع (مانند چولگی و کشیدگی) ارائه می دهند.

قضایای حدی و رفتار مجانبی متغیرهای تصادفی

نظریه احتمال شامل چندین قضیه مهم درباره رفتار مجانبی دنباله های متغیرهای تصادفی است که به قضایای حدی معروفند. دو مورد از مهم ترین این قضایا عبارتند از:

1. قانون اعداد بزرگ: بیان می کند که میانگین نمونه یی از متغیرهای تصادفی مستقل و هم توزیع (i.i.d.) با امید ریاضی μ، با احتمال زیاد به μ همگرا می شود وقتی حجم نمونه به بی نهایت میل کند.

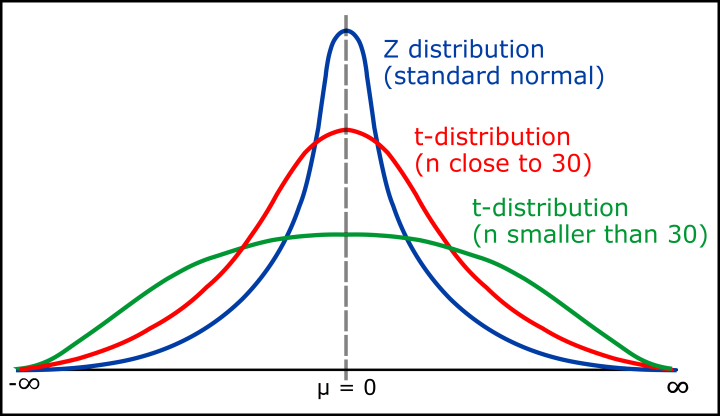
2. قضیه حد مرکزی: یکی از عمیق ترین و کاربردی ترین نتایج در نظریه احتمال است که بیان می کند تحت شرایط عمومی، مجموع (یا میانگین) تعداد زیادی از متغیرهای تصادفی مستقل، بدون توجه به توزیع اولیه آنها، تقریباً توزیع نرمال خواهد داشت.

این قضایا پایه های نظری بسیاری از روشهای استنباط آماری را تشکیل می دهند و توجیهی ریاضی برای استفاده گسترده از توزیع نرمال در آمار ارائه می دهند.

کاربردهای متغیرهای تصادفی در مدلسازی پدیده های واقعی

متغیرهای تصادفی ابزارهای قدرتمندی برای مدل سازی پدیده های تصادفی در علوم مختلف هستند. در ادامه به برخی از این کاربردها اشاره می کنیم:

در علوم مالی و اقتصاد

در مالی، قیمت سهام، نرخهای بهره و بازده سرمایه گذاری ها به عنوان متغیرهای تصادفی مدلسازی می شوند. مدل های معروفی مانند حرکت براونی هندسی برای توصیف تحولات قیمت سهام استفاده می شوند. در اقتصادسنجی، متغیرهای تصادفی برای مدلسازی رفتار مصرفکنندگان، نوسانات اقتصادی و پیشبینی شاخص های کلان اقتصادی به کار می روند.

در مهندسی و فیزیک

در مهندسی برق، سیگنال های تصادفی با متغیرهای تصادفی مدل سازی می شوند. در مهندسی عمران، بارهای وارده بر سازه ها و مقاومت مصالح به عنوان متغیرهای تصادفی در نظر گرفته می شوند. در فیزیک، حرکت براونی و نوسانات کوانتومی با استفاده از متغیرهای تصادفی توصیف می شوند.

در علوم کامپیوتر و هوش مصنوعی

در الگوریتم های تصادفی، زمان اجرا ممکن است یک متغیر تصادفی باشد. در یادگیری ماشین، متغیرهای تصادفی برای مدل سازی داده ها، نویز و عدم قطعیت ها استفاده می شوند. شبکه های بیزی که یکی از مدل های گرافیکی احتمالی هستند، بر اساس توزیع های مشترک متغیرهای تصادفی کار می کنند.

در علوم زیستی و پزشکی

در ژنتیک، توزیع صفات ارثی با متغیرهای تصادفی مدل سازی می شود. در اپیدمیولوژی، زمان ابتلا به بیماری، مدت زمان بهبودی و اثرات داروها به عنوان متغیرهای تصادفی در نظر گرفته می شوند. در طراحی آزمایش های بالینی، متغیرهای تصادفی نقش کلیدی در تخصیص تصادفی بیماران به گروه های درمانی دارند.

جمع بندی و نتیجه گیری

متغیرهای تصادفی سنگ بنای نظریه احتمال و آمار ریاضی هستند که امکان مدل سازی ریاضی پدیده های تصادفی را فراهم می کنند. در این مقاله، به بررسی جامع این مفهوم پرداختیم و دیدیم که چگونه متغیرهای تصادفی گسسته و پیوسته رفتارهای احتمالی مختلفی را نشان می دهند. توزیع های احتمال، امید ریاضی، واریانس و سایر گشتاورها ابزارهایی برای توصیف این رفتارها هستند. متغیرهای تصادفی چندبعدی امکان بررسی روابط بین پدیده های تصادفی مختلف را می دهند و مفاهیمی مانند استقلال و همبستگی به تحلیل این روابط کمک می کنند. قضایای حدی مانند قانون اعداد بزرگ و قضیه حد مرکزی رفتار مجانبی متغیرهای تصادفی را توصیف می کنند و پایه های نظری بسیاری از روش های آماری هستند. کاربردهای متغیرهای تصادفی در علوم مختلف نشان دهنده اهمیت و گستردگی این مفهوم در مدل سازی پدیده های واقعی است. درک عمیق متغیرهای تصادفی نه تنها برای مطالعه نظری احتمال ضروری است، بلکه برای کاربرد عملی آمار در حل مسائل واقعی نیز حیاتی محسوب می شود.

✨ سوال برای تفکر:

• “اگر واریانس یک متغیر تصادفی صفر باشد، چه نتیجه ای می گیرید؟”

• “چرا در بسیاری از پدیده های طبیعی، توزیع نرمال مشاهده می شود؟”

• “اگر دو متغیر تصادفی مستقل نباشند، چه تاثیری بر محاسبات آماری می گذارد؟